Reverse engineering an old Windows game for fun and compatibility

December 31, 2022  

A few months ago I decided to revisit The Last Express, one of the most unique adventure games of the 1990s. Since the version I have (from 1997) provided a Windows executable, I decided to run it using the Wayland driver for Wine. Eager to treat myself to a nostalgic journey, I ran the game and saw... nothing! I could hear the ominous menu music, but all I got was a minimized window which completely ignored my attempts at restoration. I tried the game with the Wine X11 driver and it worked as expected.

Disappointed, but also determined to get this working with the Wayland driver, I ran the game with Wine debug logging turned on. The strange minimization behavior led me to turn my attention to the SetWindowPos and ShowWindow calls, hoping that I would get some insight about what was affecting the window state. Here is what I got for the game start up, with some additional comments:

### Game window being created and resized to 640x480
trace:win:NtUserSetWindowPos hwnd 0x1005e, after (nil), 0,0 (0x0), flags 00000037
trace:win:show_window hwnd=0x1005e, cmd=5, was_visible 0
trace:win:NtUserSetWindowPos hwnd 0x1005e, after (nil), 0,0 (0x0), flags 00000043
trace:win:NtUserSetWindowPos hwnd 0x1005e, after 0xffffffff, 0,0 (1600x920), flags 00000070
trace:win:NtUserSetWindowPos hwnd 0x1005e, after (nil), 0,0 (0x0), flags 00000003
trace:win:NtUserSetWindowPos hwnd 0x1005e, after (nil), 0,0 (640x480), flags 00000050
trace:win:NtUserSetWindowPos hwnd 0x1005e, after (nil), 0,0 (0x0), flags 00000037
### Game window is minimized (6=SW_MINIMIZE)
trace:win:show_window hwnd=0x1005e, cmd=6, was_visible 1
trace:waylanddrv:WAYLAND_ShowWindow hwnd=0x1005e cmd=6
trace:win:NtUserSetWindowPos hwnd 0x1005e, after (nil), -32000,-32000 (160x24), flags 00008174

When trying to restore the minimized window I got:

### Game window is restored to 640x480...
trace:win:show_window hwnd=0x1005e, cmd=9, was_visible 1
trace:waylanddrv:WAYLAND_ShowWindow hwnd=0x1005e cmd=9
trace:win:NtUserSetWindowPos hwnd 0x1005e, after (nil), 0,0 (640x480), flags 00008120
trace:win:NtUserSetWindowPos hwnd 0x1005e, after (nil), 0,0 (640x480), flags 00000014
trace:win:NtUserSetWindowPos hwnd 0x1005e, after (nil), 0,0 (640x480), flags 00000050
### ...but then immediately minimized again!
trace:win:show_window hwnd=0x1005e, cmd=6, was_visible 1
trace:waylanddrv:WAYLAND_ShowWindow hwnd=0x1005e cmd=6
trace:win:NtUserSetWindowPos hwnd 0x1005e, after (nil), -32000,-32000 (160x24), flags 00008174

It seemed that some logic was forcing the window to always become minimized. After briefly exploring the possibility of the Wayland driver or Wine core doing something fancy, I reached the conclusion that the minimization logic lived in the application itself.

Why did the application minimize itself when running with the Wayland driver? A mystery befitting the theme of the game itself!

In order to gain more insights, I had to take a peek into the inner workings of the game. I loaded the _le.exe executable in Ghidra, analyzed it with the default options and I searched for symbols references to ShowWindow:

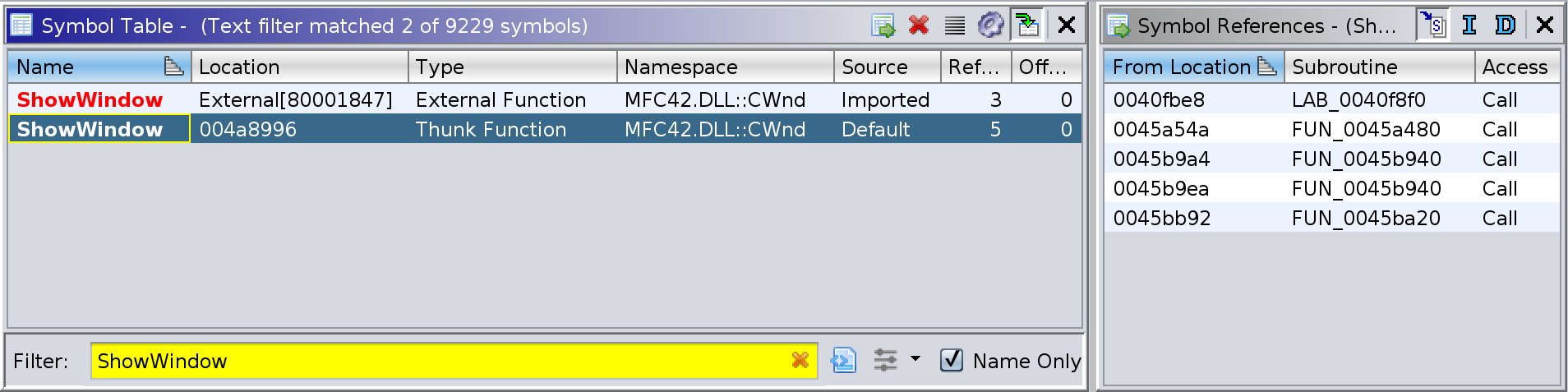
The first entry was for the location within the Import Address Table (IAT) which the dynamic linker will fill in with the address of the CWnd::ShowWindow function from MFC42.DLL.

The second entry was the CWnd::ShowWindow thunk function within _le.exe, which transfers control to the real CWnd::ShowWindow function by using the address from the IAT location described above:

004a8996 JMP dword ptr [->MFC42.DLL::CWnd::ShowWindow]

This import immediately provided a hint that the game was using Microsoft Foundation Classes, i.e., object-oriented wrappers around the Win32 API, and as such I should be on the lookout for standard object-oriented patterns.

The thunk function is what the application actually calls internally, and in the list above I could see several references to it. Alas, I checked the code at each reference location, but none was passing 6 (SW_MINIMIZE) as the show command. Could there be other references to the CWnd::ShowWindow thunk that Ghidra was missing?

I decided to get a second opinion from radare2:

$ radare2 -A _le.exe
[x] Analyze all flags starting with sym. and entry0 (aa)
[x] Analyze function calls (aac)
[x] Analyze len bytes of instructions for references (aar)
[x] Finding and parsing C++ vtables (avrr)
[x] Type matching analysis for all functions (aaft)
[x] Propagate noreturn information (aanr)
[x] Use -AA or aaaa to perform additional experimental analysis.
[0x004a8cf0]> axt 0x004a8996
(nofunc) 0x40fbe8 [CALL] call sub.MFC42.DLL_Ordinal_6215
(nofunc) 0x45a37e [CALL] call sub.MFC42.DLL_Ordinal_6215
fcn.0045a480 0x45a54a [CALL] call sub.MFC42.DLL_Ordinal_6215
(nofunc) 0x45af0e [CALL] call sub.MFC42.DLL_Ordinal_6215
(nofunc) 0x45afa7 [CALL] call sub.MFC42.DLL_Ordinal_6215
(nofunc) 0x45b018 [CALL] call sub.MFC42.DLL_Ordinal_6215
fcn.0045b940 0x45b9a4 [CALL] call sub.MFC42.DLL_Ordinal_6215
fcn.0045b940 0x45b9ea [CALL] call sub.MFC42.DLL_Ordinal_6215
fcn.0045ba20 0x45bb92 [CALL] call sub.MFC42.DLL_Ordinal_6215

There were indeed more references to the CWnd::ShowWindow thunk. I noted that the references Ghidra was missing didn't belong to any known function ((nofunc) in radare2), and that was the reason they weren't detected by default. The solution was to rerun Ghidra's analysis with the "Aggressive Instruction Finder" option turned on, which gave me the following references:

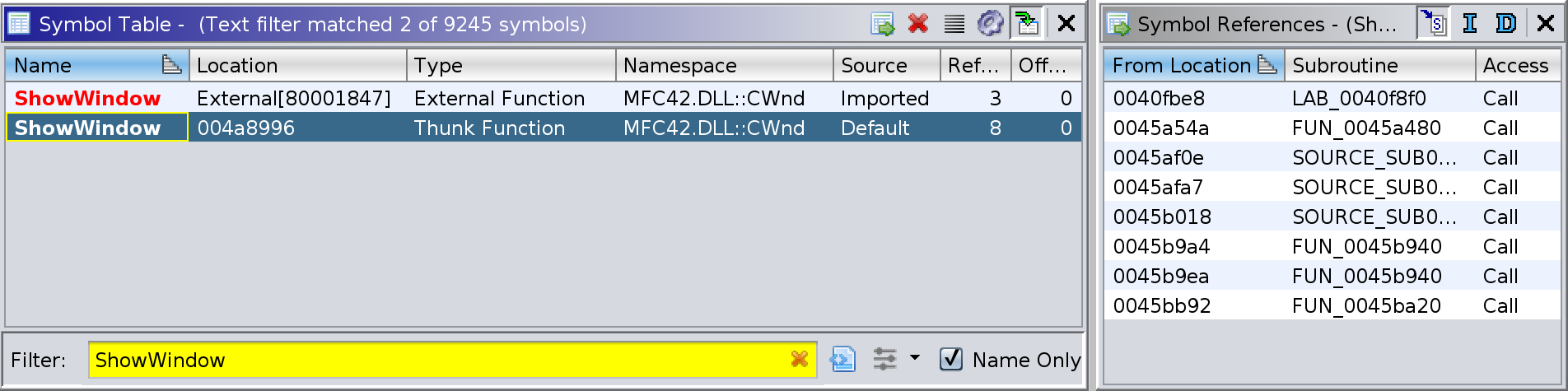
Note that the 0x45a37e reference was still missing from Ghidra. I was able to to add it by manually marking the region as code (in fact the relevant function seems to start at 0x45a340). In the end it didn't matter, though, since that particular invocation was using the 9 (SW_RESTORE) command, so was not relevant for our investigation.

From the updated reference list above there were two that involved a minimization command, at 0x45af0e and 0x45afa7. The function at 0x45ae10 which contained the 0x45af0e reference was decompiled by Ghidra as:

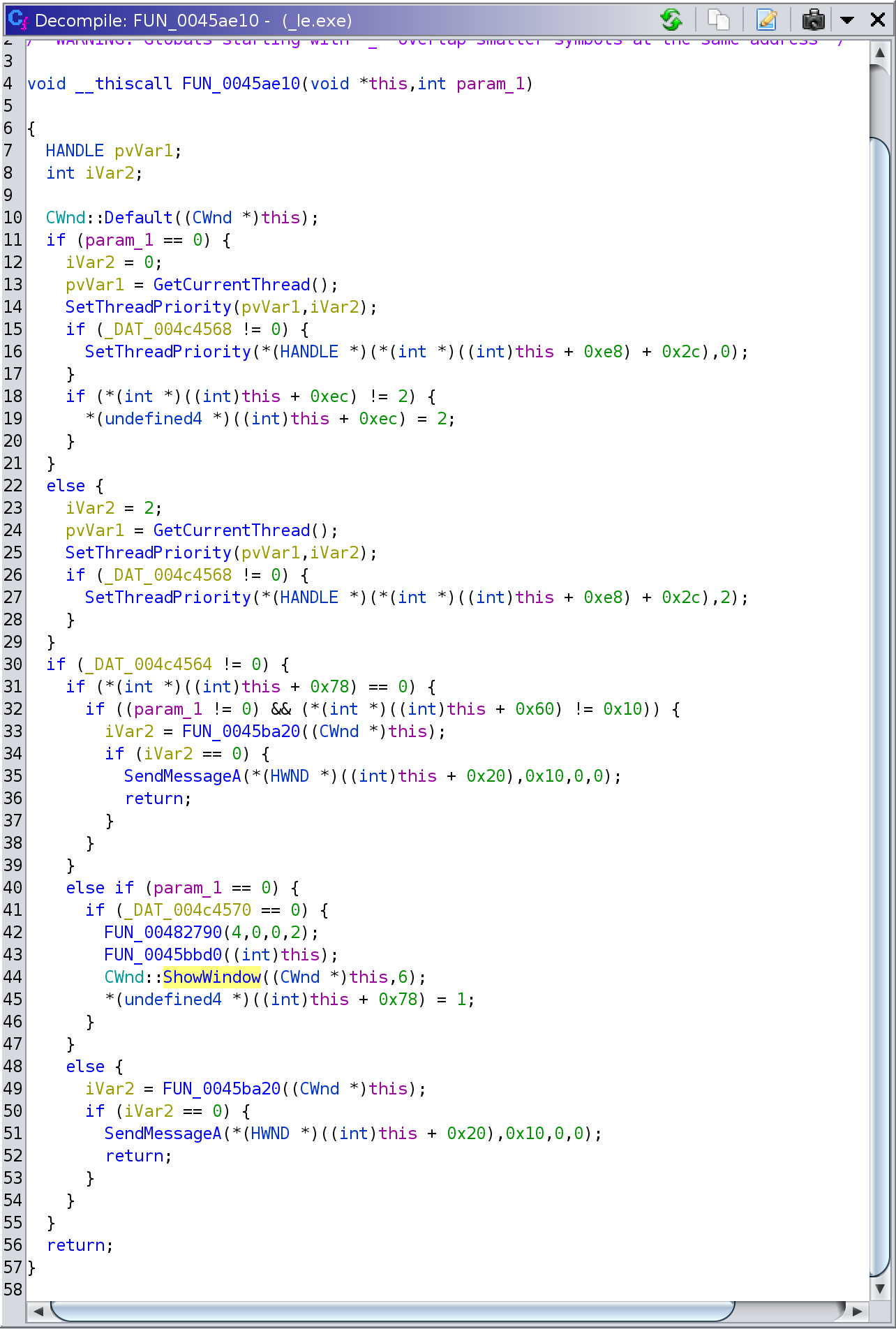
Although the high-level flow of this function was clear enough, I must say I didn't become more enlightened about the condition(s) that could lead to minimization. A quick look at some of the invoked functions indicated that a deeper investigation was required to understand how all this works, so I decided to move to the next function and revisit later, if needed.

The second reference 0x45afa7 was part of the of the 0x45af70 function:

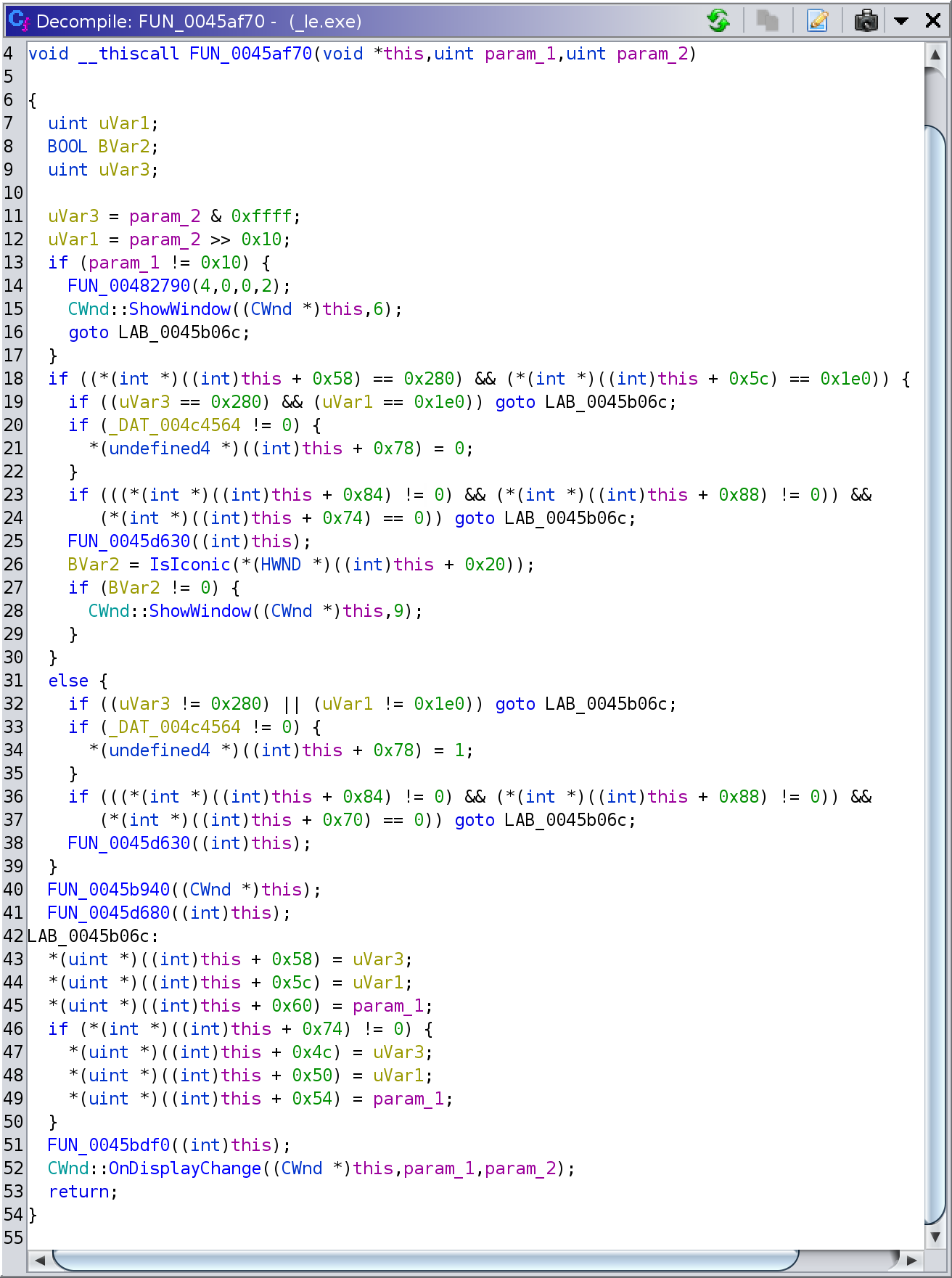
This was more promising, with a very clear check affecting minimization at the start of the function! As I could see from the decompiler output, the first argument was effectively a CWnd *. The unconditional call to CWnd::OnDisplayChange at the end allowed me to reasonably (and ultimately correctly) assume that this function was in fact an override of the OnDisplayChange method for a custom class inheriting from CWnd, so I named this function LExpressCWnd::OnDisplayChange.

The documentation for CWnd::OnDisplayChange was (and still is) surprisingly scarce online, but in a Microsoft C/C++ changelog I found the following:

CWnd::OnDisplayChange changed to (UINT, int, int) instead of (WPARAM, LPARAM) so that the new ON_WM_DISPLAYCHANGE macro can be used in the message map.

Since the game predated these changes, I determined that param_1 and param_2 were really wparam and lparam of the corresponding WM_DISPLAYCHANGE message. From the WM_DISPLAYCHANGE documentation:

wParam
The new image depth of the display, in bits per pixel.
lParam
The low-order word specifies the horizontal resolution of the screen.
The high-order word specifies the vertical resolution of the screen.

The pieces of the puzzle finally started to fall into place! Taking into account the new information I updated the decompiled source like so:

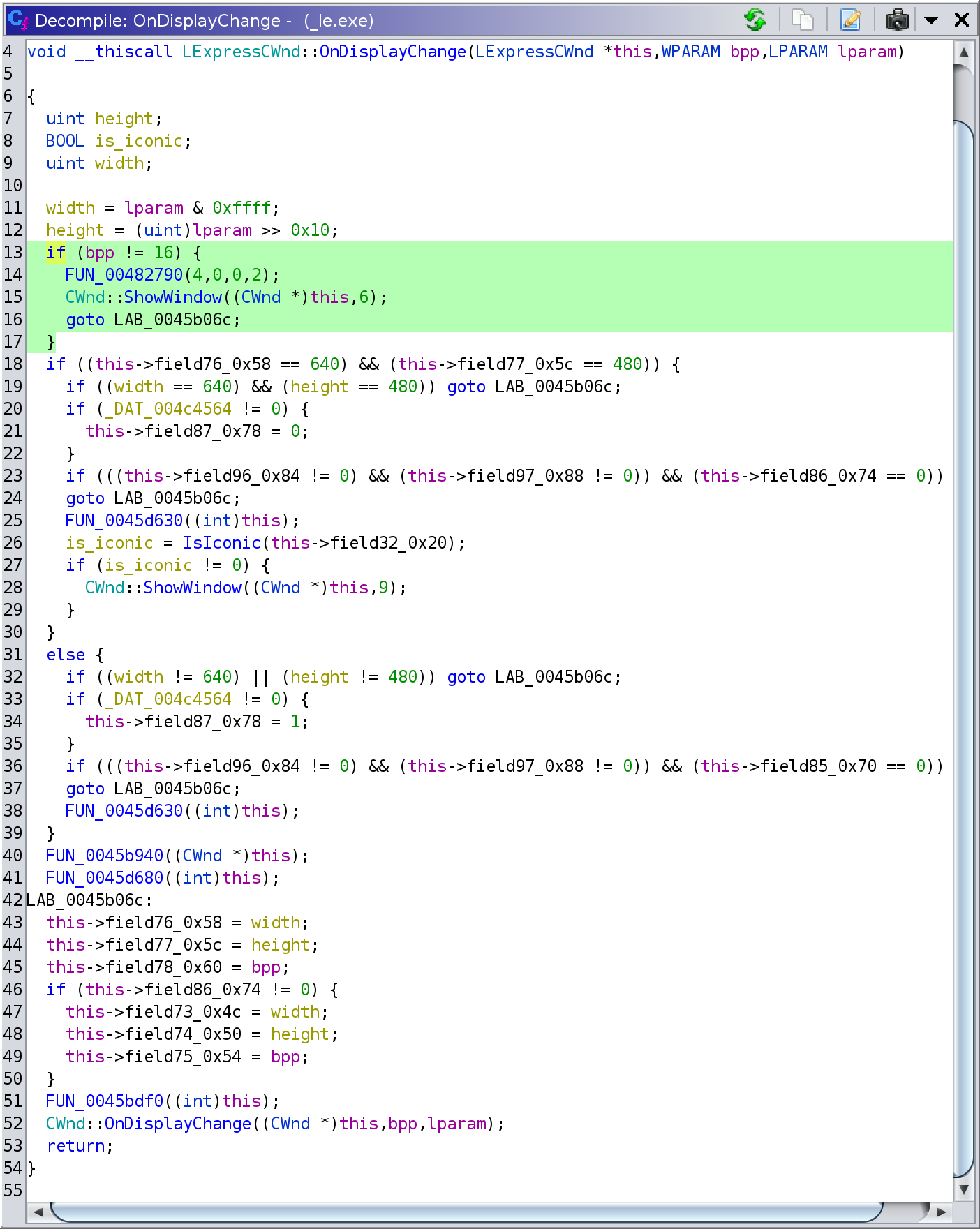
There was a lot missing still, but the main takeway, in the highlighted part of the code above, was that if the display mode was changed to one that did not use 16 bits per pixel, the application unceremoniously minimized itself!

Indeed, in that older version of the Wayland driver for Wine we were choosing a 32-bit mode regardless of what the application specified. This worked for most DirectX games since Wine internally deals with the inconsistency. However, The Last Express explicitly checks the bits per pixel value sent with the WM_DISPLAYCHANGE message and our ploy is exposed!

I updated the Wayland driver to properly set the WM_DISPLAYCHANGE bits per pixel parameter, and verified that this fixed the minimization problem. I was finally able to continue my (train) trip down memory lane!

You can see The Last Express in action with the Wayland driver here.

Bonus material

Although this partial analysis was enough to allow me to resolve the task at hand, I remained curious about some of the details of display configuration and the unexplained aspects of the LExpressCWnd::OnDisplayChange function. To explore further, I tracked symbol references to the ChangeDisplaySettingsA function from USER32.DLL and came across two invocations in _le.exe. I will spare you the details, but one reference was from a function that I determined configured the display mode for the game (which I named LExpressCWnd::ConfigureDisplay at 0x45ba20), and the other from a function that restored the original mode (LExpressCwnd::RestoreDisplay at 0x45bbd0). 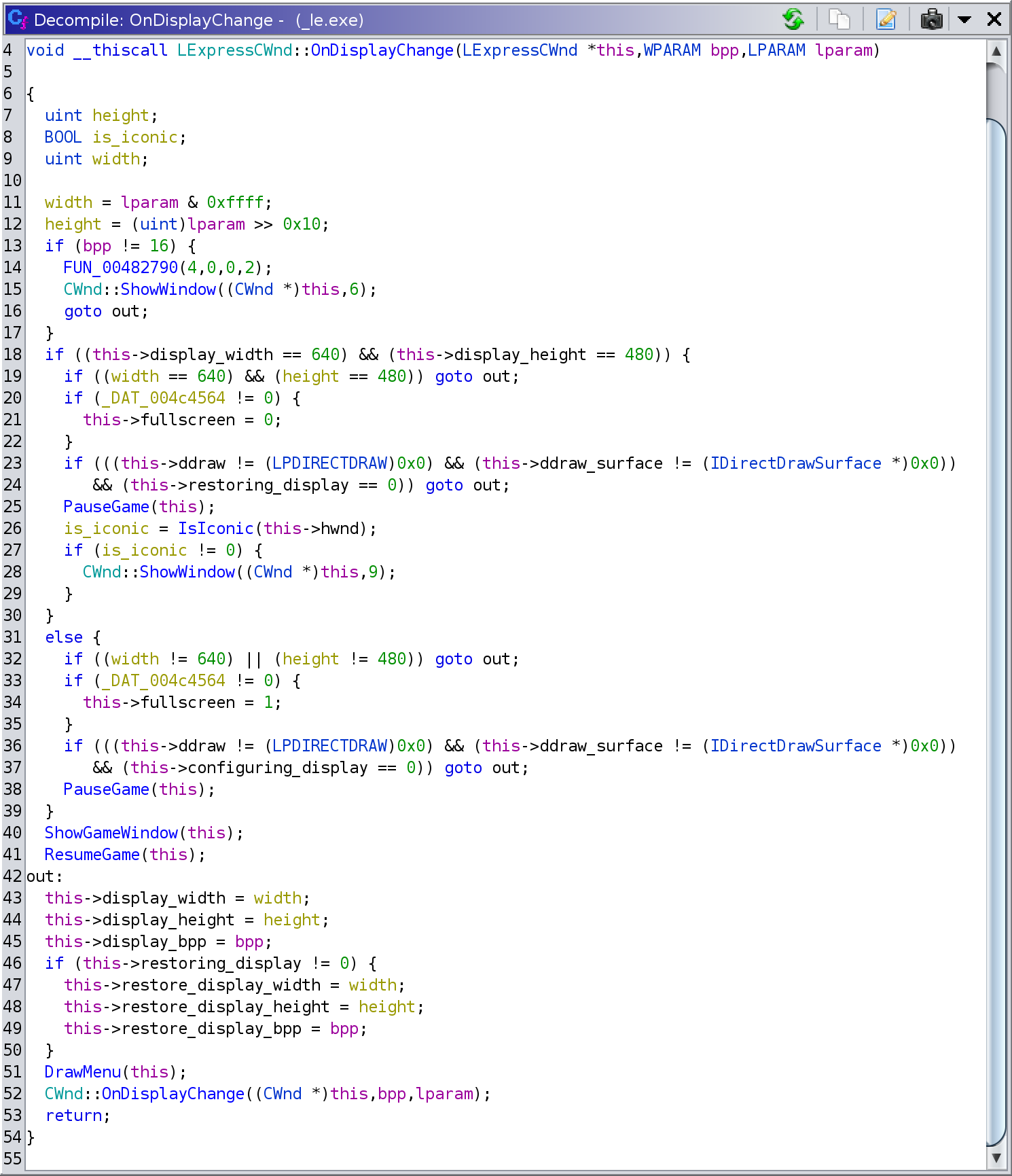One interesting point about these invocations was that the code was tracking the kind of display configuration operation the game was performing, by using fields in LExpressCWnd. For example, in LExpressCWnd::ConfigureDisplay there was the following decompiled snippet (after giving some more descriptive names):

The LExpressCWnd::configuring_display field and the corresponding LExpressCWnd::restoring_display used in LExpressCWnd::RestoreDisplay, were two of the mysterious fields used in LExpressCWnd::OnDisplayChange. The idea is that ChangeDisplaySettingsA sends the WM_DISPLAYCHANGE message synchronously, and thus LExpressCWnd::OnDisplayChange is called in the context of that invocation, reading the values of these fields.

With all this new information and a lot of additional exploration in the executable, I reached this more complete version of LExpressCWnd::OnDisplayChange:

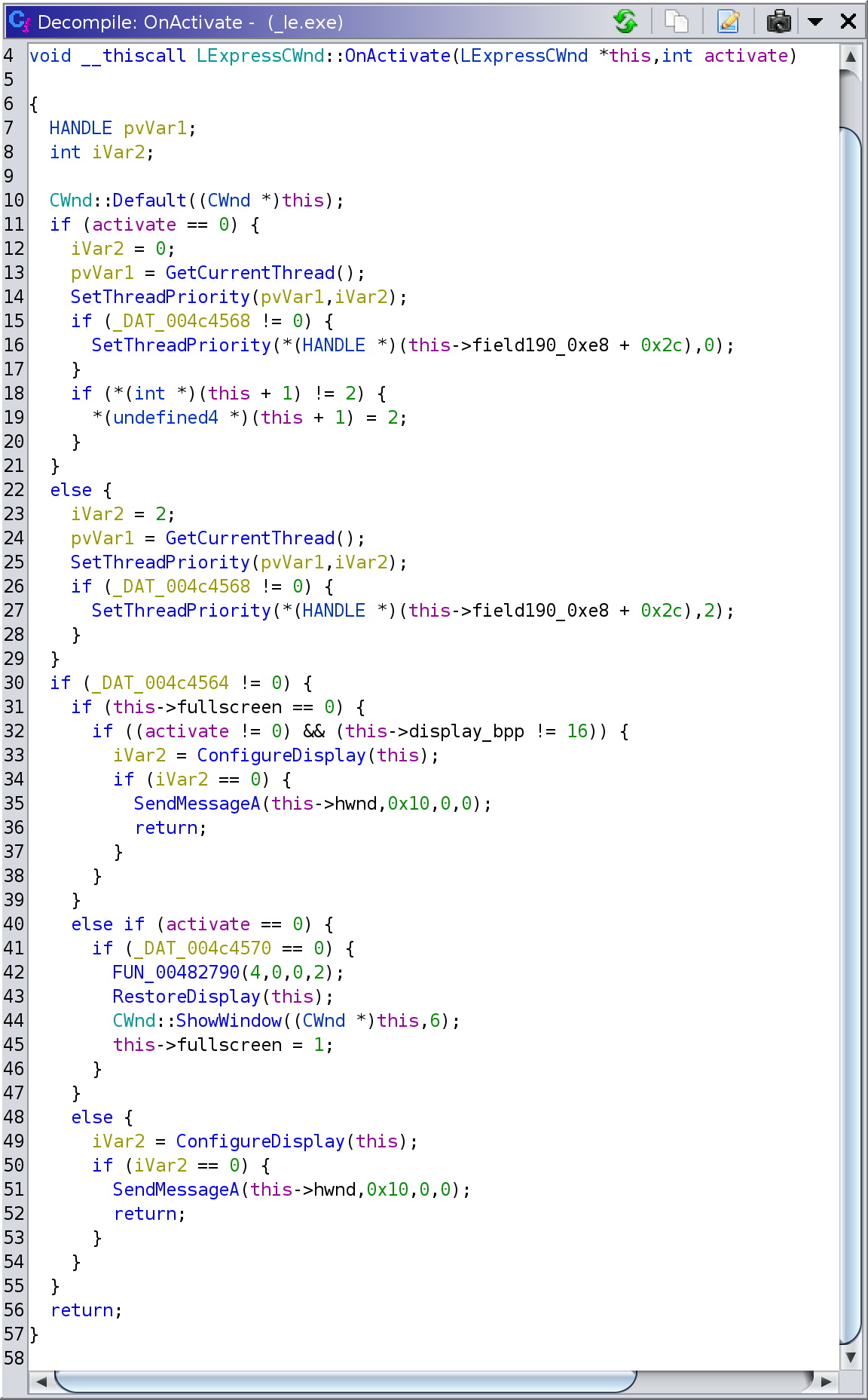
Fortuitously, the discovery of the LExpressCWnd::ConfigureDisplay/RestoreDisplay functions also helped to shed some light on the mysterious function at 0x45ae10 which we encountered earlier in this post. My best guess about that function was that it handles the (de)activation of the game window, so I named it LExpressCWnd::OnActivate. On activation it increases the game thread priority and configures the display mode (if in fullscreen mode). On deactivation it sets the game thread priority to normal, restores the display mode and minimizes the window. My final decompilation looks like:

unweave: Unweave interleaved streams of text lines

December 4, 2022  

When trying to debug unexpected behaviors in applications and libraries, I often need to understand long and complex logs. Such logs typically contain interleaved lines originating from multiple components and multiple threads and processes. In addition to the actual message content, part of the information is conveyed through the temporal relationship of the log entries.

However, such temporal relationships are sometimes hard to discern in the final interleaved output. A different view, in which each source stream of log entries is placed into its own column, can often provide more, or different, insights:

This separated, or unweaved, view has proven to be particularly useful for me in the development of the Wine Wayland driver, which is what triggered the development of the unweave tool. Since Wine logs can be very long and involve several interacting sources of information, efficiency and versatility were a primary goal of unweave.

For a practical example of unweave's capabilities, consider a log file that contains info or error output from 3 threads A, B, C:

[info] A: 1
[info] A: 2
[info] B: 1
[error] A: 3
[info] B: 2
[error] C: 1

A natural transformed view of the log involves placing each thread in its own column. This is straightforward with unweave:

$ unweave 'A|B|C' input
[info] A: 1
[info] A: 2
            [info] B: 1
[error] A: 3
            [info] B: 2
                       [error] C: 1

Typically, the output format is more complex and the relevant values not known in advance. For example, you may not know the exact thread names, only that they appear in the log in the form of $TID: where $TID is an uppercase alphabetic string. The pattern provided to unweave is a fully operational battle station regular expression, so it can handle all this too, along with making the columns wider:

$ unweave -c 15 ' ([A-Z]+): ' input
[info] A: 1
[info] A: 2
               [info] B: 1
[error] A: 3
               [info] B: 2
                              [error] C: 1

Perhaps it would be interesting to get a different view, with columns based on log types instead of threads, and also use a more distinctive column separator:

$ target/release/unweave -s ' | ' '^\[\w+\]' input
[info] A: 1 |
[info] A: 2 |
[info] B: 1 |
            | [error] A: 3
[info] B: 2 |
            | [error] C: 1

Although separating streams into columns is the primary mode of the unweave tool, it can sometimes be useful to use separate files instead, with each output filename containing the stream tag and the stream id:

$ unweave --mode=files -o 'stream-%t-%2d' 'A|B|C' input
$ tail -n +1 stream-*
==> stream-A-00 <==
[info] A: 1
[info] A: 2
[error] A: 3

==> stream-B-01 <==
[info] B: 1
[info] B: 2

==> stream-C-02 <==
[error] C: 1

Visit the unweave repository or view the manpage to find out more!

GitLab merge diffs for branches that rewrite commit history

October 22, 2022  

For the development of the Wayland driver for Wine we have been maintaining a commit series on top of upstream Wine, which we want to keep clean and easily reviewable.

For this reason, most proposed changes in the code do not typically appear as new fix commits on top of the current series, but rather transform the existing series in place, producing an updated clean version. For example, if we have the commit series a-b-c-d-e, an update may fix something in c, leading to the updated series a-b-f-d'-e' (we use d'/e' to signify that the commit introduces the same changes as d/e).

Although in this instance we have good reasons to use git in this manner, this public rewriting of commit history is not how git is typically used, and we have found that some tools do not deal too well with this scenario.

One particular pain point we have encountered is in our internal reviewing process. Although it doesn't seem possible to use GitLab to perform the actual merge of a branch that rewrites history, we would still like to get a sensible merge diff for reviews and discussion. However, when we try this we are presented with a seemingly non-sensical diff. To understand what's going on, and hopefully find a solution, we need to dive in more deeply into how GitLab, and similar tools, produce merge diffs.

Before we start our journey it would be beneficial to establish a common vocabulary for commits and operations on them. Please read the Appendix for details about the notation used in this post.

GitLab merge diffs

GitLab provides two merge diff methods, base and HEAD.

base is the older method and works by using the ... diff operator. The ... diff operator aims to provide a diff that represents the intention of the developer at the time of branching, regardless of the current state of the target branch. It achieves this by finding the most recent CommonAncestor of target and source, also called the merge base, and diff-ing the source with that ancestor. In the example below:

b is the most recent ancestor of target and source, so we get:

Diff target...source =
Diff (CommonAncestor target source)..source =
Diff b..h

Changes in the target branch after the source's branching point are effectively ignored by the ... diff.

The problem with the base method is that the produced diff contents tend to become obsolete as the merge target (which is typically the master/main branch) evolves. To make the diff more accurate the HEAD diff method was introduced.

In the HEAD method the target branch is merged into the source branch, and the resulting commit of that merge is compared with the target branch ¹.

In this case the produced diff comes from :

Diff target..(MergeInto target source) =
Diff d..m

This diff is a more accurate representation of what one would expect if the source branch was actually merged at that point in time.

However, the HEAD method may fail due to conflicts during merge, and, in this case, the current GitLab behavior is to fall back to base.

The problem

Now, let's consider what happens when we ask GitLab to provide the merge diff for our original example, trying to merge a branch fix that rewrites history, into master:

First GitLab will try the HEAD method. If the merge of master into fix succeeds then we will get a nice diff. Chances are that this merge will fail, so we will fall back to the base method. The base method will then give us git diff b..e' whereas we would like to see git diff e..e'.

Making the HEAD method work

How can we trick GitLab into producing a sane diff for our reviewing purposes? One idea is to try to make the HEAD method succeed and provide the expected results. This can be expressed by the following pseudo-equations:

Diff master..(MergeInto master fix) = Diff master..fix
Tree (MergeInto master fix) = Tree fix

If we could change that pesky MergeInto operation to become MergeIntoKeepTarget we would get our result instantly. Sadly, changing GitLab itself is outside the scope of this effort.

Not all is lost, however. We can't change MergeInto or master, but we are free to change fix (since we are the ones proposing it) to fulfill the equation. The only requirement is that the changed fix, let's call it fix', has the same tree contents as fix itself (although it may have additional merge parents).

But which fix' can we use to fulfill the above equality? There is a notable property of merging that we can make use of: if the merge target already has the merge source as a merge parent then the merge operation is a no-op. In other words the following holds:

SomeMerge2 x (SomeMerge1 x y) = SomeMerge1 x y

This property allows us to simplify our previous equation to:

Tree (MergeInto master fix') = Tree fix'

as long as fix' is of the form SomeMerge master fix. Given that we want fix' to have the same contents as fix, the decision about which merge to use is easy:

fix' = MergeIntoKeepTarget master fix

Here is what happens if we use the GitLab HEAD method to produce the diff of merging fix' into master:

Diff master..(MergeInto master fix') = Diff e..(MergeInto e m)

Since m already has e as a merge parent, MergeInto e m just gives m, so we get:

... = Diff e..m

Because MergeIntoKeepTarget gave m the same tree contents as e' we can replace one for the other in the .. diff operation:

... = Diff e..e' = Diff master..fix

Making the base method work

How about trying to bend the base method to our will? This could be useful for systems that don't support HEAD (i.e., GitHub or older versions of GitLab). This is expressed by the following pseudo-equations:

Diff master...fix = Diff master..fix // Note three vs two dot diffs
Diff (CommonAncestor master fix)..fix = Diff master..fix

As in our previous attempt, we can't change master, but we can change fix, as long as we produce a new fix' with the same contents:

Diff (CommonAncestor master fix')..fix' = Diff master..fix
Tree (CommonAncestor master fix') = Tree master AND Tree fix' = Tree fix

But which fix' can we use to fulfill the above equality this time? Another interesting property comes to the rescue: if commit x is an ancestor of y, then CommonAncestor x y = x. This provides a possible way forward: we need to make master an ancestor of fix'. The only way to change commit connections is with a merge, and we have just the merge we need, MergeIntoKeepTarget:

fix' = MergeIntoKeepTarget master fix

By a happy coincidence (or is it?) we again get the same solution as with the HEAD method!

Here is what happens if we use the GitLab base method to produce the diff of merging fix' into master:

Diff master...fix' = Diff e...m

The ancestry relationship between m and e makes the ... diff operator between them act effectively like the .. diff operator, so we get:

... = Diff e..m

Because MergeIntoKeepTarget gave m the same tree contents as e' we can replace one for the other in the .. diff operation:

... = Diff e..e' = Diff master..fix

Putting theory into practice

The theory behind our solution may be somewhat involved, but it leads to a straightforward practical recipe. It all boils down to creating the fix' commit and using that as our merge request source. Since:

fix' = MergeIntoKeepTarget master fix

we can create a detached/disposable fix' by doing:

$ git checkout --detach fix
$ git merge -sours master

Then we can push our detached fix' to our MR branch, for example by doing:

$ git push our-remote HEAD:fix

We can also verify that our solution works by locally getting the diff that GitLab will produce for the base method:

$ git diff master...HEAD

And for the HEAD method:

$ git merge master
Already up to date
$ git diff master..HEAD

Appendix: A notation for commits and their operations

In the notation used in this post each commit is represented by a letter, denoting the changes introduced by the commit. A prime (') symbol (e.g., a') denotes a commit introducing the same changes as its non-prime counterpart.

A commit series is denoted with a graph of commits, each commit pointing to its parent(s). A fork in the graph is a branching point:

A few interesting operations:

Tree x

The contents of the tree at commit x.

CommonAncestor x y

The most recent common ancestor of commits x and y. For example, in our sample commit graph we have CommonAncestor e g = c.

Diff x..y

The difference between the tree contents of commits x and y.

Diff x...y

The difference between the tree contents of commit y and base = CommonAnsestor x y.

MergeInto x y

Merges tip x into tip y, producing a new commit. For example, MergeInto e g produces the following m:

The contents of commit m are not uniquely defined. They are determined by the merge algorithm, and, in case of conflicts, by explicit user input.

MergeIntoKeepTarget x y

Merges tip x into tip y, producing a new commit which has the same tree contents as y. For example, MergeIntoKeepTarget e g gives:

In terms of git commands this operation corresponds to git merge -sours e, assuming g is checked out before the merge.

---

1. Note that the GitLab documentation, actually says that the target branch is artificially merged into the source branch, then the resulting merge ref is compared to the source branch, rather than the other way around. I believe this to be inaccurate since it contradicts both the article which inspired this feature, and my understanding of the GitLab code.